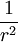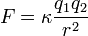Cuarto Laboratorio

CONDENSADORES O CAPACITORES

3.1 CARGA ALMACENADA Y TIEMPO DE DESCARGA DE UN CONDENSADOR

1. Arme el circuito que se muestra en la figura 3. Para ello utilice un capacitor electrolítico de 1000 μF a 16 V, un LED, una pila de 9V y una resistencia de 220 Ohm. ¿Qué tipo de capacitores se consigue en el mercado y cuál su símbolo característico?

2. Conecte inicialmente, el segmento de cable indicado con la letra A, en el orificio B del protoboard y déjelo allí durante dos (2) minutos aproximadamente.

3. ¿Cuál es el valor efectivo de la carga almacenada en el capacitor?

4. Desconecte el segmento de cable del orificio B conéctelo luego en el orificio C. Utilice un cronómetro para medir el tiempo que dura encendido el LED.

5. Calcule el periodo de descarga mediante la expresión T=C*R (C la capacitancia y R el valor de la resistencia de descarga). ¿Son iguales o hay discrepancias? Como este es un caso experimental calculen el margen porcentual de error mediante la siguiente expresión:

6. Vuelva a realizar el mismo experimento, pero en este caso conecte un voltímetro en paralelo con el LED y la resistencia; mida el potencial inicial (al instante de hacer contacto) y tome la medida de la diferencia de potencial cada diez segundos. Elabore un gráfico de V contra T (Utilice Excel o Matlab para graficar en un plano como el de la figura 4)

7. A qué tipo función matemática se parece el gráfico obtenido.

8. Repita el experimento pero con una resistencia de 1KOhm.

3.2 CAPACITORES EN PARALELO

1. Arme el circuito indicado en la Figura 5, pero con dos capacitores conectados en paralelo.

2. Aplique la misma metodología que en el anterior.

3. Calcule la capacitancia equivalente y el tiempo de descarga

4. ¿Existen diferencias significativas en los dos casos? Justifique.

3.3 CAPACITORES EN SERIE

1. Arme el circuito indicado en la Figura 6, mediante la conexión de capacitores en serie

2. Aplique la misma metodología que en el anterior.

3. Calcule la capacitancia equivalente y el tiempo de descarga

4. ¿Existen diferencias significativas en los dos casos? Justifique.

EXPERIMENTO 1.4 CAPACITOR ARTESANAL

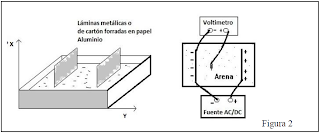
1. Construya un capacitor con dos láminas de papel de aluminio de 15 por 20 cm. Entre dichas láminas ubique un rectángulo de cartón paja (como dieléctrico), embadurnado de una crema humectante, aceite, o cualquier sustancia dieléctrica.

2. Utilice la siguiente ecuación para calcular la capacitancia del condensador artesanal.

3. Existe una técnica muy sencilla para determinar el valor de la capacitancia desconocida de un condensador, denominada puente de wheastone. Consulte sobre la manera de aplicar esta técnica y utilícela para calcular la capacitancia del condensador artesanal. Compare los dos resultados.
4. ¿Qué aplicaciones industriales y tecnológicas brinda la utilización de los condensadores? Consiga ejemplos prácticos

RESULTADO

1) a. Tipos De Condensadores Que Se Encuentra En El Mercado 

                                     

    b. Simbolos De Los Condensadores en un circuito

                          

TABLA GENERAL DE MEDIDAS DE LOS CONDENSADORES EN SERIE Y EN PARALELO

Toma De Datos Paralelo 2000 Mf

Toma De Datos serie 0.02 Mf

Toma De Datos De Un Condensador 1000 MF

Nota : Un capacitor o condensador eléctrico es un componente: 

1) eléctrico (trabaja con corrientes y voltajes),

2) pasivo (no proporciona ganancia ni excitación),

3) que acumula carga eléctrica, y

4) que puede ser simétrico (compuesto por un dieléctrico entre 2 electrodos iguales), o polarizado (con un electrolito entre dos electrodos diferentes: "+" y "-"). 

Conclusiones

*El valor C de la capacitancia es una constante del capacitor (un número real positivo) que depende de parámetros geométricos (forma y tamaño del capacitor) y físicos (del material del dieléctrico).  

*Cuando un capacitor de capacidad eléctrica C tiene una diferencia de potencial ΔV, el capacitor está cargado con una carga Q = C ΔV. La carga máxima que puede acumular está determinada por otro parámetro importante del capacitor: el voltaje máximo ΔV_max que es inferior y cercano al "voltaje de ruptura" (V_BR, Breakdown Voltage) que pueda tener sin destruirse. Este voltaje también depende de parámetros geométricos del capacitor y físicos del material dieléctrico.

*Un capacitor cargado, puede proporcionar carga eléctrica para realizar un cierto trabajo. Por lo tanto, todo capacitor cargado tiene una energía potencial eléctrica U acumulada (que se mide en "J", "joule" o "julio"). 

PARA QUÉ SIRVE 

Un capacitor es un elemento muy simple, pero según cómo y dónde se utilice, sirve para diferentes e importantes funciones

Tercer Laboratorio

CAMPO ELÉCTRICO Y SUPERFICIES EQUIPOTENCIALES

1. Arme el dispositivo que se muestra en la figura 2. Para ello se debe utilizar una caja con arena bien esparcida; dos láminas metálicas o en su defecto dos laminas de cartón forradas en papel de aluminio.

2. Conecte los bornes de una fuente de corriente continua (de unos 30 V) a cada una de las placas. Ubique la banana del negativo del voltímetro en la placa negativa y la positiva en algún lugar entre estas. Haga varias mediciones tanto de la distancia como de la diferencia de potencial o voltaje (Elabore una tabla con estos datos). Localice cinco líneas equipotenciales (misma diferencia de potencial) y trácelas sobre la arena.

3. Calcule la magnitud promedio del campo eléctrico, para una de estas superficies mediante La expresión E=Ʃ(V/r)/n ; en donde E, es el campo eléctrico, V la diferencia de potencial, r la distancia respectiva y n el número de mediciones

4. Elabore el mismo procedimiento indicado en el numeral 3 de este experimento, pero con las modificaciones que se ilustran en la figura 3.

5. ¿Qué diferencias se manifiestan entre las tres dimensiones y por qué?

Resultado

Nota :Superficies equipotenciales

Las superficies equipotenciales son aquellas en las que el potencial toma un valor constante. Por ejemplo, las superficies equipotenciales creadas por cargas puntuales son esferas concéntricas centradas en la carga, como se deduce de la definición de potencial

Segundo Laboratorio

RESISTENCIAS EN SERIE

1. Arme el circuito indicado en la Figura 11, mediante la conexión de resistencias en serie.

2. Calcule la resistencia total del circuito y mida el voltaje para cada una.
3. Cambie una de las resistencias por una de 1kΩ. Calcule la nueva resistencia total y mida nuevamente el voltaje para cada una.
4. Para cada uno de los casos anteriores calcule los voltajes totales, mediante la suma de los voltajes obtenidos para cada una en cada caso.
5. De acuerdo a lo anterior, complete el cuadro, calculando para la última celda la cantidad total de corriente que circula en cada uno de los circuitos.

Resultados

6. Corrobore para cada caso que Vp = VR1+VR2+VR3, DONDE Vp es la diferencia de potencial de la pila o batería y los demás de las respectivas diferencias.
7. Como este es un caso experimental calculen el margen porcentual de error mediante la siguiente expresión:

8. Sustituya una de las resistencias por un LED (recuerde que la pata de menor longitud debe ir conectada al lado negativo del circuito). Haga las respectivas mediciones de voltaje y corrobore la fórmula analítica.




RESISTENCIAS EN PARALELO

1. Arme el circuito indicado en la Figura 12, mediante la conexión de resistencias en paralelo.

2. Mida para cada resistencia al respectivo voltaje o diferencia de potencial.

3. Mida la resistencia total y compruebe la correspondencia con la siguiente expresión analítica
4. Dicho resultado es mayor menor o igual que el de cada una de las resistencias indicadas? Justifique.
5. Sustituya una de las resistencias por otra de 1KΩ y repita nuevamente los procedimientos anteriores.
6. Mida la intensidad de corriente del circuito (Amperaje), y la que circula por cada una de las resistencias (para ello se desconecta por uno de los lados la resistencia indicada, y se completa el circuito haciendo puente con los bornes del multímetro)
7. Corrobore que IT=I1+I2+I3, donde IT es la intensidad de corriente medida para todo el circuito; y en caso de inconsistencia aplique la formula de margen de error utilizada en la práctica anterior.
8. ¿Qué son los puertos LPT y cual su utilidad, ventajas y desventajas frente a los COM?
9. Las instalaciones telefónicas domiciliarias presentan un tipo de configuración para ser eficientes. Conecte dos teléfonos en serie y luego en paralelo, pida para cada caso que la hagan una llamada y verifique de manera directa en cual de los dos casos cual configuración es mejor. Explique con argumentos válidos. En cual de los dos casos hay mayor consumo y por qué?
10. Conecte un LED entre R3 y el borne negativo. ¿Cómo es su brillo cada vez que se van quitando resistencias? Justifique.

Resultados

 

Primer Laboratorio

1. Para el desarrollo de este experimento se requiere de los siguientes materiales: un 

electroscopio sencillo como el que se muestra en la figura 1, una lámina u objeto de 

plástico, una lámina metálica pequeña o un rectángulo de cartón envuelto en papel 

aluminio, un lápiz u objeto de madera y un paño tela o tejido de lana.

Resultados 

1. Al frotar el objeto plástico (regla)  con el paño y acercarlo al centro de las  dos esferas de icopor, el objeto plástico induce una carga positiva y las esferas de icopor  inducen una carga negativa lo cual produce que las cargas negativas de las dos bolas de icopor  sean atraídas por la carga positiva de el plastico

Los materiales con los que tratamos en nuestra vida diaria están formados por átomos y moléculas que son eléctricamente neutros porque tienen el mismo número de cargas positivas (protones en el núcleo) que de cargas negativas (electrones alrededor del núcleo). El fenómeno de la electricidad estática requiere de una separación sostenida entre las cargas positivas y negativas

Los electrones pueden ser intercambiados entre dos materiales por contacto y, además, los materiales que tienen unos electrones débilmente ligados tienen tendencia a perderlos mientras que los materiales que no tienen llenas las capas externas de electrones tienen tendencia a ganarlos. Este fenómeno es conocido como triboelectricidad y da como resultado que uno de los objetos que se han puesto en contacto quede cargado positivamente mientras el otro se carga negativamente. La polaridad y la cantidad de la carga neta que queda a cada material cuando se separan dependerá de sus posiciones relativas en la serie triboeléctrica (una lista que clasifica los materiales en función de su polaridad y su capacidad de adquirir carga). El efecto triboeléctrico es la causa principal de la electricidad estática que observamos en nuestra vida diaria e incluye la que se produce por rozamiento de diferentes materiales.

2. Para descargar el electroscopio basta tocar la esfera con la mano, es decir se establece 'contacto con tierra' a través de nuestro cuerpo.

3.

para calcular la fuerza de atracción y/o repulsión usamos la ley de Culomb

En la barra de la balanza, Coulomb colocó una pequeña esfera cargada y a continuación, a diferentes distancias, posicionó otra esfera también cargada. Luego midió la fuerza entre ellas observando el ángulo que giraba la barra.
Dichas mediciones permitieron determinar que:

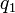• La fuerza de interacción entre dos cargas y duplica su magnitud si alguna de las cargas dobla su valor, la triplica si alguna de las cargas aumenta su valor en un factor de tres, y así sucesivamente. Concluyó entonces que el valor de la fuerza era proporcional al producto de las cargas:

    y     en consecuencia:

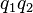
• Si la distancia entre las cargas es , al duplicarla, la fuerza de interacción disminuye en un factor de 4 (2²); al triplicarla, disminuye en un factor de 9 (3²) y al cuadriplicar , la fuerza entre cargas disminuye en un factor de 16 (4²). En consecuencia, la fuerza de interacción entre dos cargas puntuales, es inversamente proporcional al cuadrado de la distancia:

Asociando ambas relaciones:
Finalmente, se introduce una constante de proporcionalidad para transformar la relación anterior en una igualdad:

4. Rayo

El rayo es una descarga electrostática natural.

El rayo es un ejemplo de una descarga electrostática que se puede observar en la naturaleza. Aunque los detalles no están del todo claros, se considera que la separación de las cargas está relacionada con el contacto que se produce entre las partículas de hielo que forman los nubes de tormenta. Pero sea cual sea la causa, el rayo resultante no es otra cosa que una versión a gran escala de las chispas que podemos observar en las descargas electrostáticas domésticas. La emisión de luz por la descarga calienta el aire que hay alrededor del canal que sigue la corriente eléctrica y lo hace hasta una temperatura que produce luz por incandescencia. El sonido del trueno es el resultado de la onda de choque que se crea por la rápida expansión del aire sobrecalentado.